I was curious about the probabilities and have an unhealthy fascination with spreadsheets, so I committed this. https://docs.google.com/spreadsheets/d/1C_TK-gNLCzmJ5vQ__FKmhE_751Phx4GtSxePJuaTRKQ/edit?usp=sharing
(Apologies if this info was posted before and I overlooked it.)

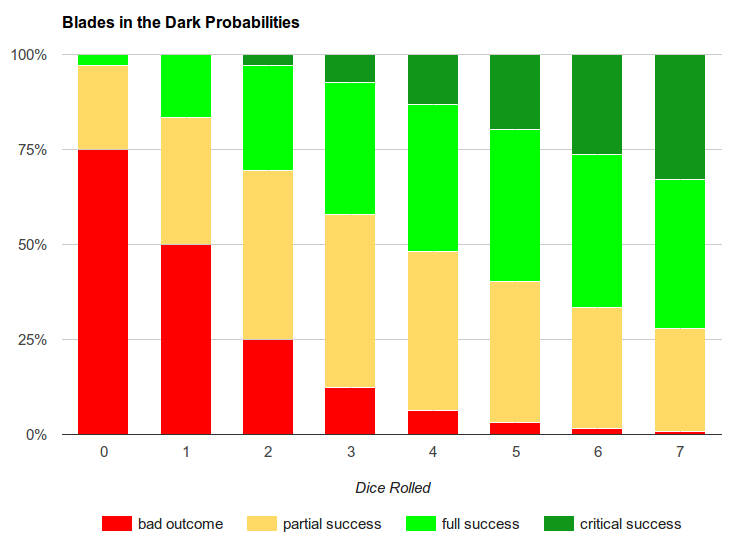
I ran some some of these numbers as well, (having this in a graph is awesome) I found it surprising how linear they are. It’s good for players to be aware of this, every die is more valuable than it might seem at first!
You mean exponential.
I don’t actually, you would expect it to be, and for the diminishing returns to be really pronounced, (and technically it is probably exponential) but if you look at rate the chance between partial success and full success changes as you add dice, it’s surprisingly close to linear for all reasonable numbers of dice. It’s pretty cool.
More clearly, by the time the exponential diminishing returns on the odds for a particular result level start being apparent, the odds for the next highest result are approximating a linear progression in their odds, so adding more dice continues to be worthwhile.
The bad result is clearly decaying exponentially 1/2^d. Similarly the probability of success or critical success is exponentially increasing 1-(5/6)^d. All of this is blatantly obvious looking at the first 3 die results.
Christopher Rinderspacher
All of that is completely true! Which is why I said its SURPRISING how (close to) linear the results are. I guess I should be more careful about omitting words like that. 😛 I am also a math guy so I understand being frustrated by people using the term exponentially inappropriately.
Nice. I’m not that good at the math so while I tried I didn’t get anything as lovely as this. It’d be neat to see variants of this for each position that delineates success vs failure and danger manifesting. I know that’s awkward because some results offer choice, but still, it’d be neat.
The graphs are exactly the same, regardless of position. Red is 1-3, yellow is 4-5, light green is 6, and dark green is crit.
My only nitpick is terminology, but I think its the source of a lot of problems in play. 4-5 is not a partial success! It’s a full success with danger.
The terminology comes from page 6, “Rolling the Dice”.
Adam, if I understand you correctly, you’re asking for things like, “Assuming I always chose ‘You do it’ if it’s an option, what’s the likelihood by position and dice of getting “you do it”. Ultimately it would amount to coloring the same blocks in different ways. Depending on how you interpret “You do it with reduced effect,” your odds might be better with Risky than Controlled, oddly.
Right Alan De Smet Not only probability of “You do it” in each position but also how that pairs with the probability of whether danger manifests or not.
Really awesome spreadsheet. I took it a bit further – there’s some fun arithmetic for critical successes. What’s interesting is the optimum points – where outcome probabilities are at their maxima. This is 3 dice for partial success and 6 dice for full success (zero dice for bad outcome and infinite dice for critical success, BTW). This would imply (to me) that at start of play you should always try to boost your best skills with fine items, assists, devil’s bargains and so forth.
Oh, and everything except critical success is Poisson-distributed (or some related pdf).